前回(こちら)は、さいころの1の目が出る確率が1/6であるとき「6回に1回1が出るとは限らない」ということを示しました。今回は、「では確率が1/6であるとはどういう意味か」を考えていきます。
前回は、確率が1/6ということから6回振ってみましたが、今回はもっと多くの回数を振ってみます。その振った回数の中で、1の目が何回出る可能性が高いか調べます。
1から6までの番号の書いてあるさいころを、今度は全部で$N$回さいころを振る。
問1:1が1回出る確率を求めよ。
問2:1が$m$回出る確率を求めよ。
問3:問3で$m$を1から$N$まで足し合わせ、1が少なくとも1回出る確率を計算せよ。
答えです。
問1:1が1回だけ出るということは、他の$N-1$回では確率5/6で1でないものが出るということである。ここまでで確率を計算すると。$$\left(\frac{1}{6}\right)^1\left(\frac{5}{6}\right)^{N-1}$$ となる。1が出る場所について、1番目、2番目、…、$N$番目の$N$通りがあるので、これをかければよい。$$N\left(\frac{1}{6}\right)^1\left(\frac{5}{6}\right)^{N-1}$$ これが答えである。
問2:1が出る場所が複数あったら、N個の試行のうちその場所を選ぶ組み合わせを考えればよい。このことと、1が$m$回、そうでないのが$N-m$回出るということから$${}_{N}C_m\left(\frac{1}{6}\right)^m\left(\frac{5}{6}\right)^{N-m}=\frac{N!}{m!(N-m)!}\left(\frac{1}{6}\right)^m\left(\frac{5}{6}\right)^{N-m}$$が答えとなる。
問3:ちょっとおまけで出してみました。\begin{eqnarray}
\sum_{m=1}^{N}{}_{N}C_m\left(\frac{1}{6}\right)^m\left(\frac{5}{6}\right)^{N-m} &=&\left(\frac{5}{6}\right)^N\left[-1 + \sum_{m=0}^{N}{}_{N}C_m\left(\frac{1}{5}\right)^m\right] \\
&=&\left(\frac{5}{6}\right)^N\left[-1+\left(1+\frac{1}{5}\right)^N\right] \\
&=&1 – \left(\frac{5}{6}\right)^N
\end{eqnarray}
となります。ただし、途中で2項定理
\begin{align}
(1+x)^N = \sum_{m=0}^N{}_NC_mx^m
\end{align}
を使っています。この計算結果は、前回の問の結果と同じになっています。
さいころの1の目は何回出やすいのか?~二項分布~
特に問2に着目してください。全部で$N$回サイコロを振ったとき1の目が$m$回出る確率は\begin{align}{}_NC_m\left(\frac{1}{6}\right)^m\left(\frac{5}{6}\right)^{N-m}\end{align}でした。$m$の値に応じてこの値はどのように変わるでしょうか?実際にグラフを書いて確認してみます。
例えば$N=8$の時は$m$の値によって下のように確率の値を変えます。
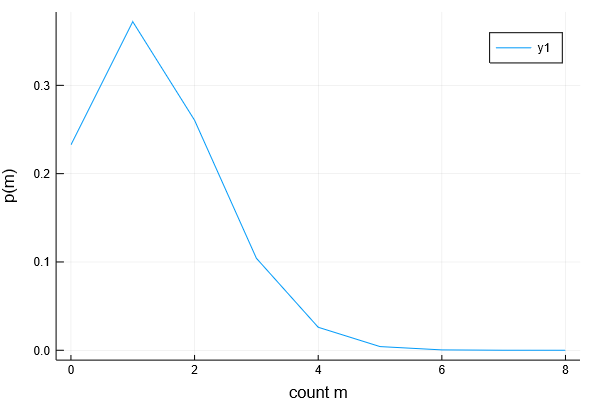
このような確率分布を2項分布といいます。全部で8回サイコロを振るときは、1は1回だけ出る確率が大きいというところでしょうか。
さらにさいころを振る回数を増やした時、この値はどうなるでしょうか?計算すると次の図のようになります。回数$N$を8、20、200、2000とし、横軸は回数mを全体の回数Nでわったm/N、縦軸は確率$p(m)$に$\sqrt{N}$をかけて$\sqrt Np(m)$として、比べています。
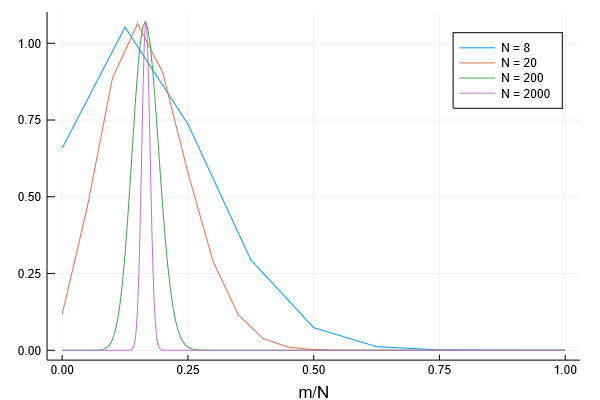
グラフを見ると、$m/N$はある値のところによって集まっているように見えます。その値とは何でしょうか?
実は、ここが$1/6=0.1666…$という値です。
以上をまとめると、
さいころを、「ものすごくたくさん」振ったときに、1が出る回数はその1/6程度になる可能性が十分高くなる。
\begin{align}
\frac{1が出た回数}{さいころを振った回数(たくさん)}\sim\frac{1}{6}
\end{align}
ということになります。
以上を俯瞰して
私たちが「確率」を習うとき、以下のように習うかと思います。
「確率は、物事の起こりやすさを表す数である。以下のように計算する。
\begin{align}(確率)=\frac{注目している事象の場合の数}{全事象の場合の数}\end{align}」
あくまで、「さいころの1の目が出る確率が$\frac16$である」といったときのその計算方法は、事象の場合の数に拠っているのであって、「6回さいころを振る」という意味ではないのです。
では、この確率の値が「見える形」で現れるのはどのようなときかというと、非常に多くの回数の試行を行って、注目している事象が起こる割合に着目したときということになります。
\begin{align}\frac{注目している事象が起こった回数}{全試行回数}\end{align}
の値が、全試行回数を十分に大きくしていくと、その事象の確率に近づいていきます。これを大数の法則といいます。
次回は上の2項分布が、さいころを振る回数が大きくなるにつれてどうなるか具体的に計算をし、対数の法則を導出してみます。
