前回はこちら
本日は、前回の2項分布が、さいころを振る回数を大きくすることによってどうなるかを調べます。
今回は問題なしで、また数式メインになります。
下のグラフが前回も出した通り、横軸が1の目が出た回数$m$を全体の試行回数$N$でわったもの、縦軸が1が$m$回出る確率に$\sqrt{N}$をかけたものになっています。
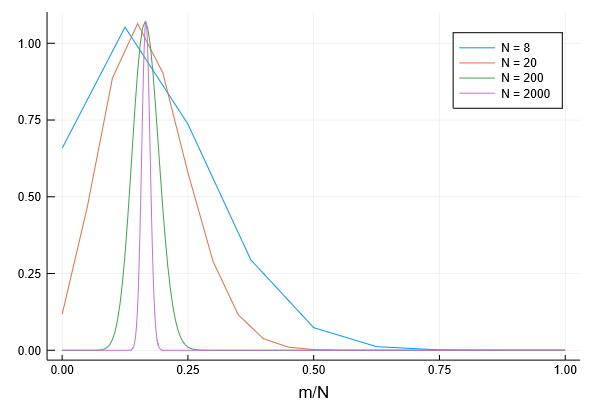
二項分布は正規分布に近づく
正規分布とは、確率変数$x$(さいころの例でいえばさいころを振る回数や、それを全体の回数$N$で割ったもの)に対する確率密度$p(x)$が$e^{-ax^2}$の形になるもの、具体的には
\begin{align}
p(x) = \frac{1}{\sqrt{2\pi\sigma}}\rm{exp}\left[-\frac{(x-m)}{2\sigma^2}\right]
\end{align}
の形になるものをいいます。$m$が平均値、$\sigma$が分散にあたります。平均値近くの確率が高くなり、そこから分散$\sigma$の値以上離れたところでは確率はほぼ0に近いです。
実は、2項分布は、試行回数$N$が十分大きいと、正規分布に近くなります。
計算
今まではさいころの1が出る回数を考えていたので1回でそうなる確率を$1/6$としていたが、もう少し一般的に考えたい。確率$p$の事象があって、これが$N$回中$m$回起こったとする。その確率を$P(m)$とする。$q=1-p$とする。
$P(m)$は二項分布となり、
\begin{align}
P(m) = {}_NC_mp^mq^{N-m} = \frac{N!}{m!(N-m)!}p^mq^{N-m}
\end{align}
スターリングの公式$n!\fallingdotseq\sqrt{2\pi n}(n/e)^n$を使って
\begin{align}
P(m) &= \frac{\sqrt{2\pi N}(N/e)^N}{(\sqrt{2\pi m}(m/e)^m)(\sqrt{2\pi(N-m)}((N-m)/e)^{N-m})}p^mq^{N-m} \\
&= \frac{1}{\sqrt{2\pi}}\sqrt{\frac{N}{m(N-m)}}\frac{N^N}{m^m(N-m)^{N-m}}p^mq^{N-m}\\
&= \frac{1}{\sqrt{2\pi Npq}}\left(\frac{pN}{m}\right)^{m+1/2}\left(\frac{qN}{N-m}\right)^{N-m+1/2}
\end{align}
$\left(\frac{pN}{m}\right)^{m+1/2}\left(\frac{qN}{N-m}\right)^{N-m+1/2}$を正規分布の形にできないか考える。そこで、以下の手順で$\rm{exp}(-)$の形を出現させてみる。
2.1.で出た値を近似する。
3.expの中に戻す。
ここで、
\begin{align}
x=\frac{m-pN}{N}
\end{align}とおく。これはこのページ一番上のグラフの横軸にあたり、グラフの山(が出ると期待されるところ、$=p$)を原点$x=0$としている。この値$x$は、$0$にすごく近い小さいところで効いてくるだろうと考えられる。$m=(x+p)N$、$N-m=(-x+q)N$より
\begin{align}
\ln(\sqrt{2\pi Npq}P(m)) &= \ln\left[\left(\frac{p}{x+p}\right)^{N(x+p)+1/2}\left(\frac{q}{-x+q}\right)^{(q-x)N+1/2}\right]\\
&= (N(x+p)+1/2)\ln\left(\frac{p}{x+p}\right)+(N(q-x)+1/2)\ln\left(\frac{q}{-x+q}\right)
\end{align}
$N(x+p)+1/2$や$N(q-x)+1/2$において$N$を十分大きくするので$1/2$を無視する。
\begin{align}
\ln(\sqrt{2\pi Npq}P(m)) &= N(x+p)\ln\left(\frac{p}{x+p}\right)+N(q-x)\ln\left(\frac{q}{-x+q}\right)\\
&= -N(x+p)\ln\left(1+\frac{x}{p}\right)-N(q-x)\ln\left(1-\frac{x}{q}\right)
\end{align}
今ここで、$x$はすごく小さいところで左辺が大きくなると考えているので、$x/p$、$x/q$は小さいとみる。そうすると対数関数は
\begin{align}
\ln(1\pm x)=\pm x – \frac{1}{2}x^2 + O(x^3)
\end{align}
と近似できる。$O(x^3)$は$x$の3次以上の項である。
\begin{align}
\ln(\sqrt{2\pi Npq}P(m)) &= -N(x+p)\left(\frac{x}{p}-\frac12\left(\frac{x}{p}\right)^2\right)-N(q-x)\left(-\frac{x}{q}-\frac12\left(\frac{x}{q}\right)^2\right)+O(x^3)\\
&= -\frac{N}{2pq}x^2 + O(x^3)
\end{align}
よって2項分布は
\begin{align}
P(m)\fallingdotseq \frac{1}{\sqrt{2\pi Npq}}\rm{exp}\left[-\frac{N}{2pq}\left(\frac{m-Np}{N}\right)^2\right]
\end{align}
となり、中心を$Np$、分散を$\sqrt{pq/N}$とする正規分布に近づく。$P(m)$は$N$を大きくしていくと$m=Np$を中心に集まっていきそのほかの値では$0$に近づいていく。$m/N=p$ゆえ以上をまとめると
試行回数$N$を十分大きくすると、確率$p$の事象が起こった回数を$m$として$m/N\fallingdotseq p$となっている。(試行回数が小さかったらこうなるとは限らない。)
大数の法則
実は、このことは一般的に「大数の法則」とよばれます。
平均$\mu$、分散$\sigma^2$の分布があるとする。互いに独立した確率変数$X_1,X_2,…,X_N$があったとき、任意の正の数$\epsilon$に対し$\{X_i\}$の平均が$\mu$の$\epsilon$近傍から外れる確率は、$N$を限りなく大きくすることで0にできる。
\begin{align}
\lim_{N\to\infty}Prob\left(\left|\frac{X_1+X_2+…+X_N}{N}-\mu\right|>\epsilon\right)=0
\end{align}
補足:ここで述べた大数の法則は、より正確に言えば大数の弱法則になる。
