以下の問題をやってみましょう。
下にマス目があります。1マスの縦と横の長さはそれぞれともに1とします。格子点同士を結んで正方形を書きます。例えば、下の図のように正方形を書くことができ、その面積は10です。
問1:面積2の正方形を書きなさい。
問2:面積13の正方形を書きなさい。
問3:面積7の正方形を書きなさい。
問4:面積1から20までの正方形を、書けるものは書きなさい。
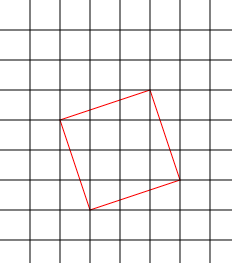
答え
今回は、主に問4を1つ1つ確かめていこうと思います。
まず、面積1の正方形はもちろん書けますね。

面積2の正方形も以下のように書くことができますが、面積3の正方形は書けません。

面積4の正方形、面積5の正方形は書けますが、面積6の正方形は書けません。
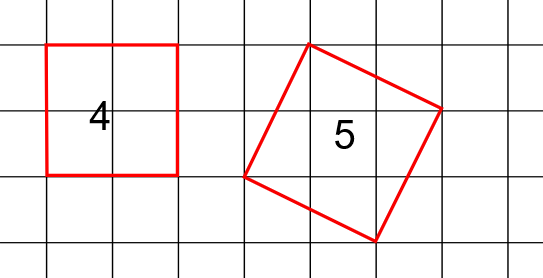
以下同様にして、面積20までは以下の正方形が書けます。これら以外の面積の正方形は書けません。
(問3の答えは、「なし」です。)

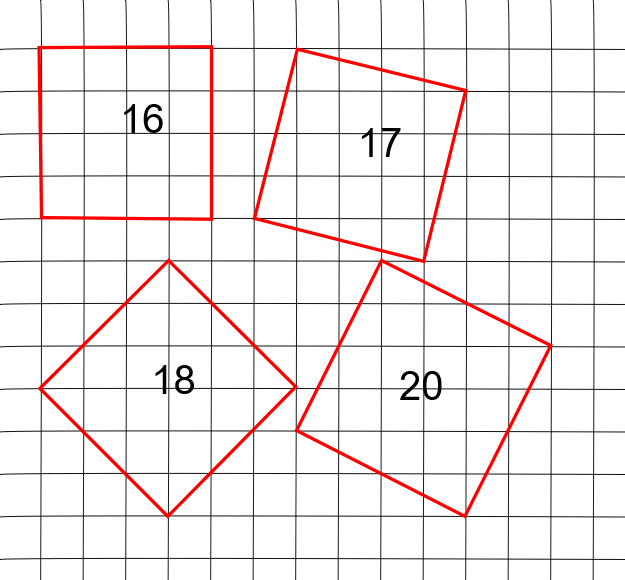
格子点を結んで書ける正方形の面積
では、以上を見ると、1、2、4、5、8,9、10、13、16、17、18、20$\cdots$という面積の正方形であれば格子点を結んで作ることができることが分かりました。これらに法則はあるのでしょうか。考えてみようと思います。
まず、正方形の1辺の位置を適当に決めます。この時、以下のように縦幅を$a$、横幅を$b$とします。

正方形の1辺の位置を決めれば、正方形の形はただ一つに決まります。(位置は4通りあり得るけど)

この正方形の一片の長さ$c$は三平方の定理より
\begin{align}
c^2=a^2+b^2
\end{align}
となります。よって正方形の面積は
\begin{align}
(中の正方形の面積)=c^2=a^2+b^2
\end{align}
よって、面積が$n$になるような正方形があるためには
であることが同値です。
4で割った余りに着目する。
まず、簡単な考察として「4で割った余り」に着目します。
整数$a$とその2乗$a^2$を4で割った余り($a\ (mod\ 4)$、$a^2\ (mod\ 4)$)は以下のようになります。
| $a\ (mod\ 4)$ | $a^2\ (mod\ 4)$ |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 0 |
| 3 | 1 |
よって、$a^2+b^2$を4で割った余りは、以下の4通りが考えられます。
| $a^2\ (mod\ 4)$ | $b^2\ (mod\ 4)$ | $a^2+b^2\ (mod\ 4)$ |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 2 |
よって、$a^2+b^2$を4で割った余りが3になることはあり得ないです。よって、4で割って3余る整数は、平方数の和で書けないことが分かりました。実際、格子点を結んでできる正方形の面積に、3、7、11、15、19は入っていません。
今後の流れ
では4で割って3余る整数でなければ、すべて平方数の和で書けるでしょうか?格子点を結んでできる正方形の面積をみてみると、例えば6、14などもそれぞれの面積の正方形を作れないことが分かります。よって、その整数が平方数の和で書けるために、「4で割って3余る整数以外」という条件だけでは不十分だということが分かります。
より強い条件を求めるため、その整数を「素数」か「合成数」かに分けます。「素数」の時は、「4で割って3余る整数以外」という条件で十分になっています。「合成数」の時は少し複雑な条件になっています。
ここら辺の話を次回以降で展開していきます。
